Muscoli antigravitari: si oppongono davvero alla forza di gravità?
dott. Mauro Lastrico dott.ssa Laura Manni
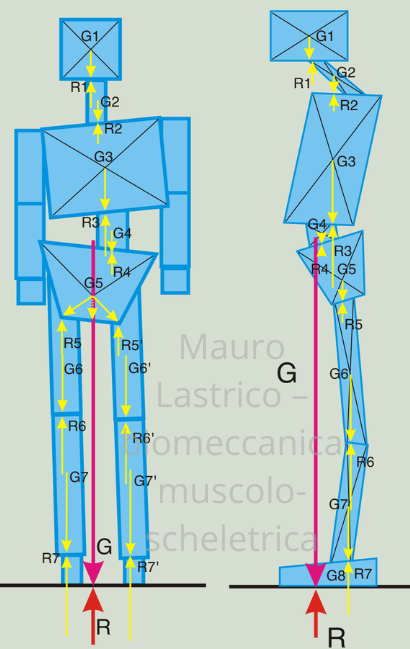
Il termine “muscoli antigravitari” viene comunemente utilizzato per indicare i muscoli che si oppongono alla forza di gravità. In realtà, la forza di gravità (forza peso) è costantemente bilanciata dalla controspinta del suolo.
L’obiettivo del sistema muscolare non è opporsi alla gravità, ma verticalizzare i singoli baricentri corporei lungo la verticale della controspinta, consentendo una distribuzione equilibrata dei carichi lungo la colonna vertebrale e le articolazioni degli arti.
Quando l’organizzazione muscolare è alterata, i baricentri si disallineano rispetto alla verticale della controspinta: aumentano le compressioni articolari e cresce il tono necessario per mantenere l’equilibrio.
Abstract
L’equilibrio del corpo umano non può essere interpretato come una condizione statica o come il semplice mantenimento di una postura “corretta”, ma come il risultato dinamico dell’interazione tra le forze fisiche che agiscono sul sistema muscolo-scheletrico. In particolare, la gravità e le reazioni vincolari generano un campo di forze che deve essere continuamente gestito attraverso l’organizzazione muscolare e scheletrica.
Nel modello biomeccanico analitico e sistemico, l’equilibrio emerge dalla corretta distribuzione delle forze e dall’allineamento funzionale dei baricentri segmentari, piuttosto che da un controllo volontario o da un assetto morfologico ideale. Le alterazioni dell’equilibrio non vengono quindi attribuite a deficit di controllo, ma a modificazioni prevedibili delle relazioni meccaniche tra i segmenti corporei.
Gli accorciamenti muscolari e le variazioni del tono basale influenzano direttamente la gestione delle forze gravitazionali, modificando la risultante dei carichi e le modalità di trasmissione delle forze lungo la catena scheletrica. L’equilibrio diventa così un indicatore funzionale dello stato meccanico del sistema, sensibile sia alle alterazioni locali sia alle riorganizzazioni sistemiche.
Documento PDF
Il documento PDF approfondisce i principi fisici alla base dell’equilibrio del corpo umano, analizzando in particolare:
-
il ruolo della gravità come interazione fisica
-
il rapporto tra forza peso e reazioni vincolari
-
la distribuzione delle forze nei segmenti corporei
-
il concetto di baricentro e di allineamento funzionale
-
l’influenza degli accorciamenti muscolari sull’equilibrio
-
le implicazioni biomeccaniche sulla statica e sulla dinamica
(Il bottone di download del documento è disponibile sotto il titolo della pagina.)
Collocazione teorica del documento
Il documento presentato costituisce un capitolo del volume in uscita
Biomeccanica Muscolo-Scheletrica – Analitica e Sistemica. Principi di Fisica Applicata per la Pratica Clinica,
e fornisce i fondamenti fisici necessari per comprendere l’equilibrio umano come fenomeno biomeccanico, governato da leggi universali.
Il testo non propone modelli di controllo motorio né strategie di allenamento dell’equilibrio, ma definisce i criteri interpretativi per leggere le alterazioni dell’equilibrio come conseguenze di modificazioni meccaniche misurabili e prevedibili.
Relazione con il modello biomeccanico analitico e sistemico
Nel modello biomeccanico analitico e sistemico, l’equilibrio rappresenta l’espressione macroscopica dell’organizzazione delle forze all’interno del sistema muscolo-scheletrico. La sua analisi consente di:
-
collegare la distribuzione dei carichi agli accorciamenti muscolari
-
interpretare le variazioni dell’assetto corporeo senza ricorrere a concetti posturali
-
comprendere il rapporto tra equilibrio, statica e dinamica
-
integrare l’analisi locale all’interno di una visione sistemica
Il Metodo Mézières, nella rielaborazione AIFiMM, utilizza questi principi come base interpretativa per l’analisi clinica delle disfunzioni muscolo-scheletriche.
Applicazioni formative del modello
I principi fisici e biomeccanici dell’equilibrio descritti nel documento vengono approfonditi e applicati nei percorsi formativi AIFiMM, in particolare: