Perché si crea un conflitto articolare: cause biomeccaniche e squilibrio muscolare
dott. Mauro Lastrico - dott.ssa Laura Manni
Il conflitto articolare è una condizione frequente associata a dolore, limitazione del movimento e sovraccarico articolare. Alla base del conflitto sono spesso presenti cause biomeccaniche legate allo squilibrio muscolare e alla distribuzione non uniforme delle forze muscolari intorno all’articolazione.
Quando le forze muscolari non sono bilanciate, alcune superfici articolari ricevono maggiori pressioni, aumentano le compressioni articolari e si instaurano condizioni favorevoli al sovraccarico progressivo.
L’analisi biomeccanica delle forze consente di comprendere perché si crea un conflitto articolare, individuando l’origine meccanica del problema e distinguendo le cause primarie dai compensi secondari.
Abstract
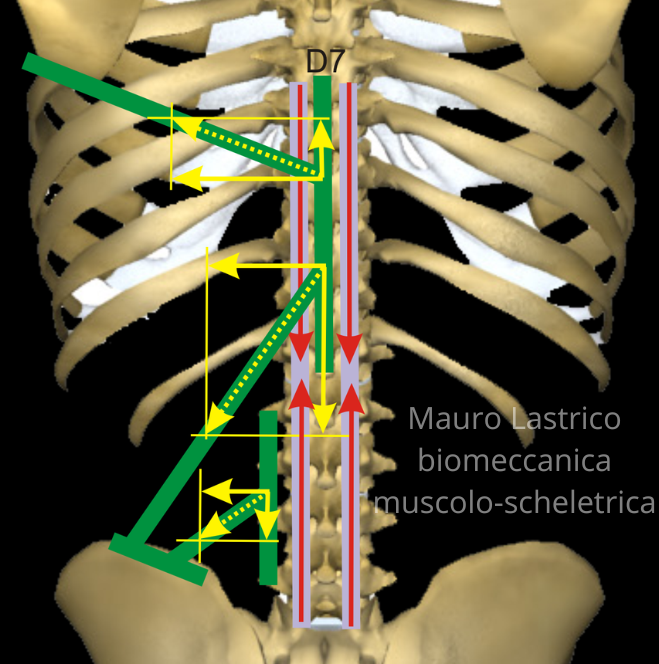
L’analisi vettoriale rappresenta uno degli strumenti fondamentali per la comprensione dei fenomeni biomeccanici che regolano il comportamento del sistema muscolare. Ogni muscolo, attraverso la propria linea d’azione, genera un vettore di forza che interagisce con quelli prodotti dagli altri muscoli, determinando equilibri, disequilibri e adattamenti strutturali del sistema muscolo-scheletrico.
Nel modello biomeccanico analitico e sistemico, il muscolo non viene considerato come un’unità isolata, ma come parte di una rete di relazioni vettoriali interdipendenti. L’assetto meccanico di un distretto o dell’intero sistema emerge quindi dalla risultante delle forze in gioco, piuttosto che dall’azione di un singolo elemento.
L’analisi vettoriale consente di descrivere in modo rigoroso le dominanze muscolari, i vettori primari e secondari, e le modificazioni progressive degli equilibri meccanici dovute agli accorciamenti muscolari. Questo approccio permette di interpretare le alterazioni della statica e della dinamica come conseguenze prevedibili di variazioni nelle relazioni di forza, superando una lettura puramente descrittiva delle disfunzioni.
Documento PDF
Il documento PDF approfondisce l’analisi vettoriale applicata al sistema muscolare, sviluppando in particolare:
-
il concetto di muscolo come vettore di forza
-
le relazioni vettoriali tra muscoli agonisti, antagonisti e sinergici
-
la distinzione tra vettori dominanti e sottodominanti
-
l’effetto degli accorciamenti muscolari sulla risultante delle forze
-
le conseguenze biomeccaniche sui segmenti articolari
-
il passaggio dall’analisi distrettuale all’interpretazione sistemica
(Il bottone di download del documento è disponibile sotto il titolo della pagina.)
Collocazione teorica del documento
Il documento presentato costituisce un capitolo del volume in uscita
Biomeccanica Muscolo-Scheletrica – Analitica e Sistemica. Principi di Fisica Applicata per la Pratica Clinica,
e fornisce gli strumenti matematici e biomeccanici necessari per interpretare il comportamento del sistema muscolare come sistema complesso di forze interagenti.
L’analisi vettoriale rappresenta uno degli elementi chiave che consentono di collegare le leggi della fisica applicata alla biomeccanica con l’osservazione clinica, rendendo possibile una lettura coerente e prevedibile delle disfunzioni muscolo-scheletriche.
Relazione con il modello biomeccanico analitico e sistemico
Nel modello biomeccanico analitico e sistemico, l’analisi vettoriale costituisce il passaggio logico che permette di:
-
identificare le dominanze muscolari
-
comprendere l’origine dei disassiamenti articolari
-
interpretare la sequenza degli adattamenti compensativi
-
distinguere tra fenomeni primari e secondari
Il Metodo Mézières, nella rielaborazione AIFiMM, utilizza questi principi come base interpretativa per l’analisi clinica e la scelta dell’intervento, senza ridurre il modello a schemi rigidi o protocolli predefiniti.
Applicazioni formative del modello
I principi di analisi vettoriale del sistema muscolare vengono sviluppati e applicati nei percorsi formativi AIFiMM, in particolare: