Biomechanics: Vector Analysis Applied to the Muscular System

Extract from:

"Musculoskeletal Biomechanics and Mézières Methodology"
Author: Dr. Mauro Lastrico
Marrapese Publisher

Linear and nonlinear mathematics
The Mézières method is based, both for evaluation and application, on physical-mathematical concepts.
 

Linear mathematics

In mathematics the concept of linear means that two functions have a direct relationship (linear function). Linear algebra is the branch of mathematics that studies vectors, vector spaces (or linear spaces), linear transformations and systems of linear equations.
A system is defined as linear if the elements composing it can be decomposed and recomposed and if in it the increase of one variable corresponds to a proportional increase of another (e.g. expansion of a bar due to heat).
Linear systems have simple equations admitting analytic solutions.
Linear algebra studies all physical "linear" phenomena, that is, those intuitively not involving distortions, turbulence and chaotic phenomena in general.
In short, we could say that linear mathematics, "approximating the system", is a representation of reality that allows understanding of its functioning.
The musculoskeletal biomechanical analysis proposed in this text foresees the transformation of muscle bundles into compressive force lines and, to these, their vector actions on skeletal components will be applied.
There will be, that is, a vectorial type analysis.

Vector analysis
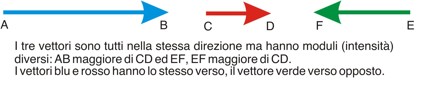
In physics, a vector is a geometric element characterized by three elements:
* magnitude: it is its intensity (graphically represented by the length of the segment)
* direction: the line on which the vector lies
* sense: the direction along the line (graphically expressed with an arrow).
It is indicated by a segment oriented from A to B.
It is called "Vector" because in a certain sense it transports A to B.

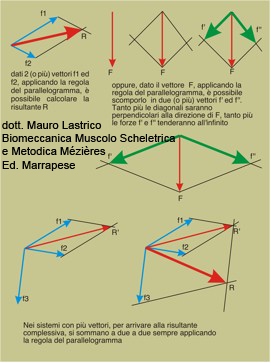
Using the parallelogram rule it is possible to calculate the resultant between two or more vectors. The parallelogram rule is also applicable in the opposite sense to decompose a given vector into two or more components according to the desired direction.
In systems with many acting forces to arrive at the overall resultant the forces are summed two by two always applying the parallelogram rule.

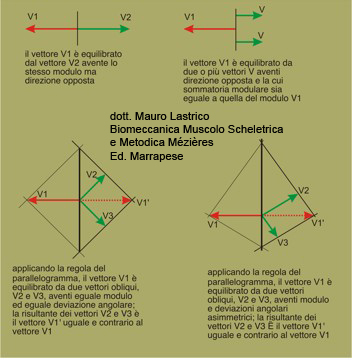
The parallelogram rule is also used to calculate the intensity that one or more vectors must express to balance another based on their arrangement in space.

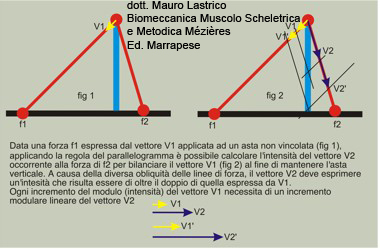
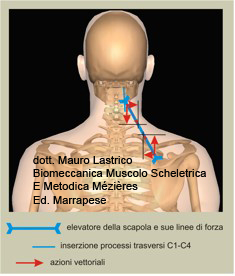
Articular axiality, in addition to capsulo-ligamentous structures, is ensured by the balancing of acting muscular forces.
In most joints, vectorial potentials between agonists and antagonists are asymmetric and vector calculation allows to establish which forces are dominant and with what intensity subdominant forces must express themselves to balance the dominant ones.
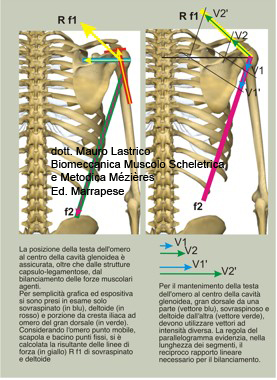
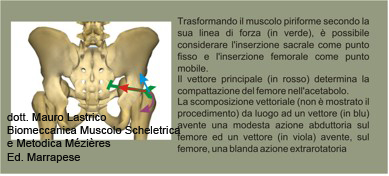
In the example shown in the figure, the associated forces of the deltoid and supraspinatus opposed to those of the portion extended from humerus to iliac crest of the latissimus dorsi were taken into consideration.
Calculated the resultant force line between deltoid and supraspinatus that determines the elevation of the humerus, it was compared to the force line of the latissimus dorsi that depresses the humerus.
The seated position of the humerus is equivalent to the rod in the previous figure.
Compared to the rod, that is the seated position of the humerus inside the glenoid cavity of the scapula, the overall force line of deltoid and supraspinatus has a lower angle than the force line of the latissimus dorsi, that is less oblique.
Consequently, to balance any vectorial intensity expressed by the latissimus dorsi, deltoid and supraspinatus must respond with an almost double vectorial intensity.
In the simplified example, for greater graphical and expository clarity, not all muscles were taken into consideration, the latissimus dorsi is dominant and deltoid and supraspinatus subdominant.

In the images, muscles will be represented not in their anatomical reality but according to their lines of force and vectors will be applied to these.
The line of force of a muscle is essentially given by the arrangement of the fibers.
Vectors can be represented either through their resultant or, through the decomposition procedure, through their components.
Vector forces will determine skeletal movements.

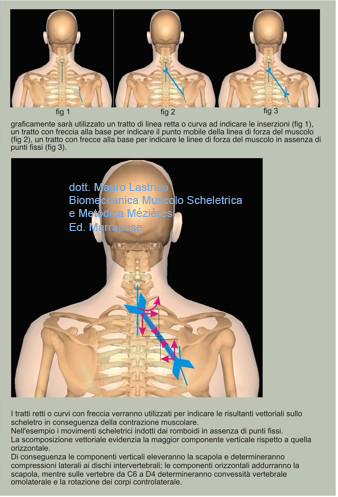
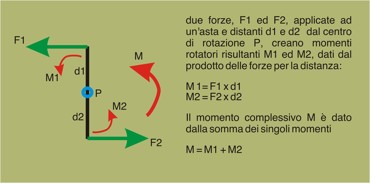
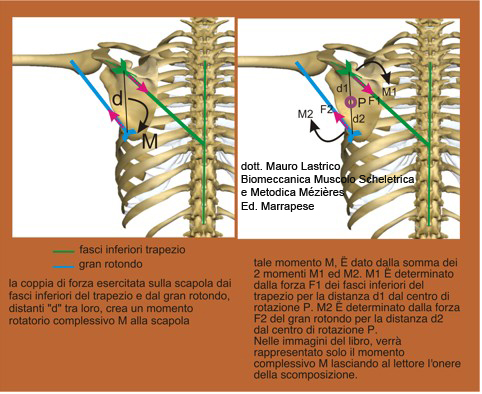
However, not always one resultant is reached, especially if we consider the three-dimensional plane. When at least two resultants are present we talk about a "couple of forces".
Couples of forces generate resulting "moments". The moment is given by the product between the magnitude (intensity) of the forces and their distance.

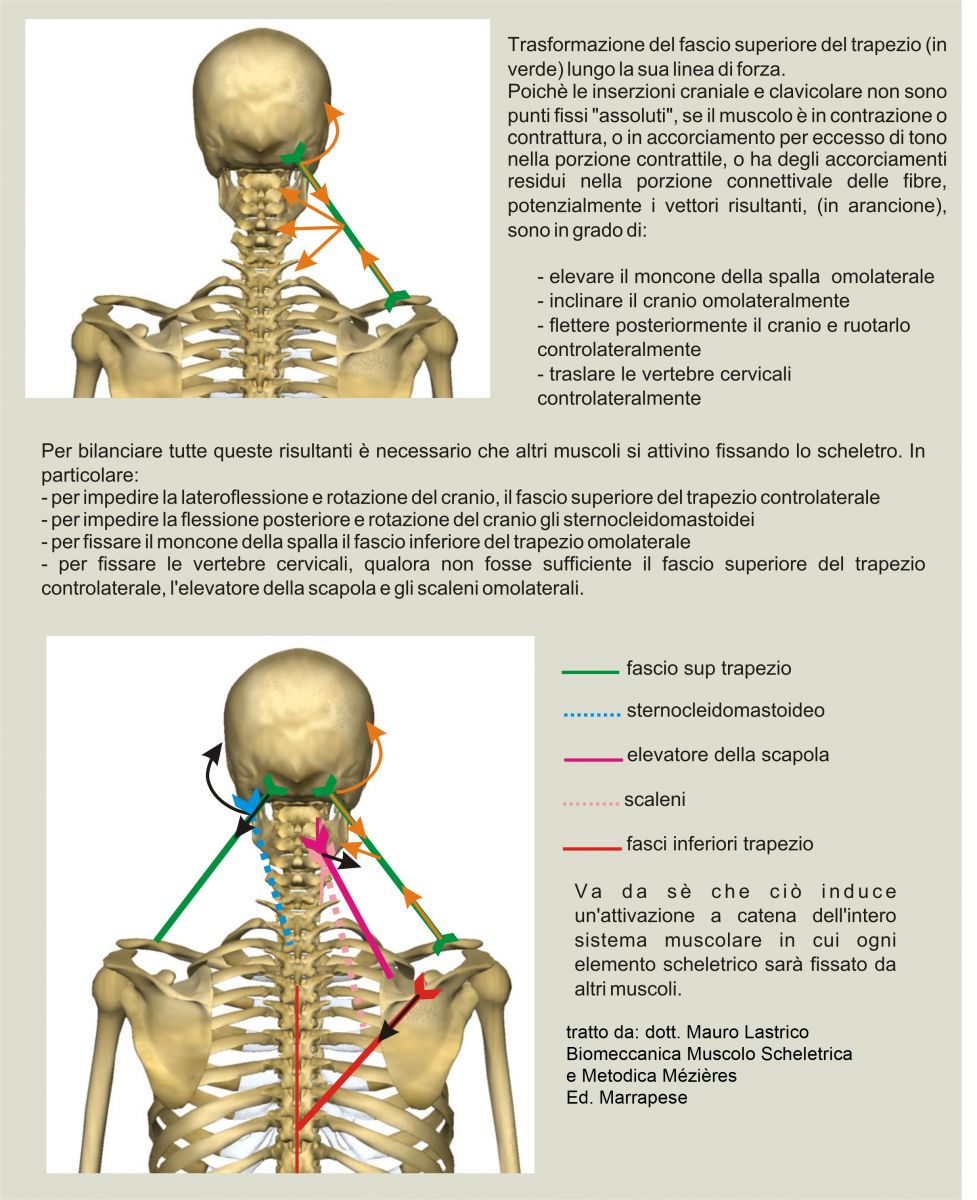
Applying vector logic to muscles it is necessary to consider that muscles act by bringing insertions closer together and that, therefore, during contraction they determine a double compressive force line.
This is more true for polyarticular muscles and for those with insertion on mobile skeletal portions. For monoarticular muscles with fixed skeletal insertions (the pelvis for example) it is possible to consider them as forces having a single direction.

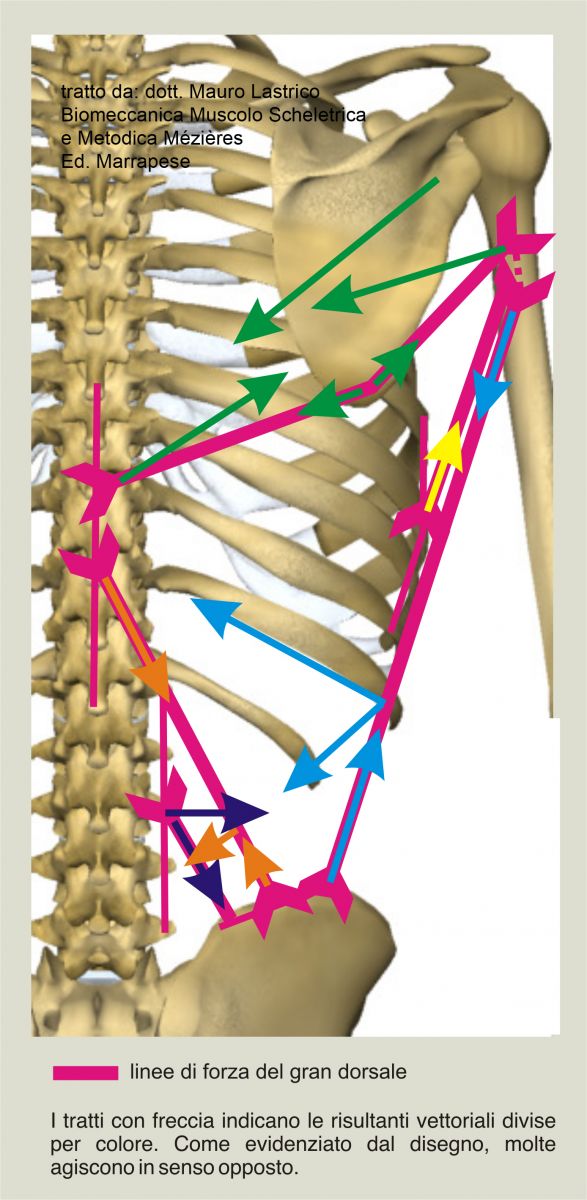
In the above figure the dashed lines indicate the anterior insertion with respect to the posterior view of the image.
If then a large polyarticular muscle such as the latissimus dorsi is taken into consideration, the vector decomposition highlights the multiplicity of actions this muscle is able to perform.

The analytical treatment of muscular actions on skeletal components will be addressed in the chapter "Biomechanics"

Nonlinear mathematics
While in linear mathematics there is a proportional relationship between stimulus and effect, in nonlinear mathematics it is possible to obtain large variations even with small signals.
This means that alterations that in linear mathematics would be considered negligible, in nonlinear mathematics can be relevant to the overall functioning of a system.
Nonlinear mathematics deals with studying real behaviors through general interpretive models. 
Among the many components of nonlinear mathematics we will refer in particular to complex systems.
Complex systems
A "complex system" is any system composed of more than one element or subsystem and has various characteristics including:
1. in a complex system all elements composing it are interdependent and interacting;
2. understanding the functioning of a complex system can only take place by considering the system as a whole;
3. a complex system, in pursuing its objectives, is able to generate solutions not predictable from examining the individual elements, that is, it is able to generate "emergent abilities";
4. a complex system makes the best use of its energy when it stands at the "edge of chaos", that is when the elements of stability and dynamism are in such equilibrium as to allow small signals to modify the state of the system "guiding" different behaviors and therefore saving energy.

By integrating the two "mathematics" it will be possible to study "analytically" the local functioning mechanisms and at the same time have "general" interpretative tools on the factors regulating "posture".