Biomechanics of Static Vector Muscle Analysis

Extract from:

"Musculoskeletal Biomechanics and Mézières Methodology"
Author: Dr. Mauro Lastrico
Marrapese Publisher

This text will consider alterations of the physiological joint sequence caused by a shortening involvement of the muscular system.
Similar patterns may be induced by congenital or acquired problems and specific pathologies. To avoid repeating the distinction each time, this eventuality will be taken for granted. Therefore, in the discussion, reference will be made to intact muscles, normally innervated, and absence of specific pathologies of the musculoskeletal system or other origin.

Whatever the symptom, expressed as pain or functional impotence or their combination, in the examined area there is an alteration of the physiological joint sequence or dysmorphism, detectable through specific investigative tools and through the objective examination comparing the ideal posture with that of the patient.
Since muscles do not behave in isolation but are part of a complex system, morphological alterations will not only be found in the symptomatic district but extended, micro or macro, to all joints.
The proposed biomechanical investigation considers muscles as vectors of compressive force, progressively losing ideal length.
The analysis of shortening effects will be both systemic and analytical: overall all muscles shorten but with different intensities.
Muscles, besides movement, have an important role in joint stability and have, with respect to the joint, different disposition and length.
Vectorially, the greater the length of the muscle, the greater its capacity to exert tensile force.
In the absence of specific pathological patterns, the muscle length cannot anatomically be greater than physiological: during an action, the antagonist muscle is stretched compared to the initial position and acts as a brake to the joint excursion, but if the movement is within the joint range, such stretching will respect the maximum potential physiological length (figs. 1 and 2).

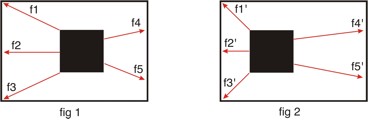
In fig. 1, the black square is maintained in its position inside the outer square through the cocontraction of all forces acting from f1 to f5.
The forces are not symmetrically distributed and if all increase the intensity of the tensile force, the black square inside the white square (fig. 1), will move as in fig. 2.
All forces from f1' to f5' are in excess tension: f1', f2' and f3' vectorially prevail and are shortened, f4' and f5' oppose the tensile force, increase tone, but compared to the original position they are stretched.
Such stretching, however, does not exceed the maximum capacity, since the movement of the black square is within the limit given by the outer square.
To bring the black square back to the central position it will not be necessary to further increase the force expressed by f4' and f5', but to create the conditions so that all forces from f1' to f5' (in particular f1', f2' and f3') decrease their intensity, returning to the initial state from f1 to f5.
Consequently, any human movement that is within the joint range will cause a passive stretching of the antagonists, a stretching that will not, however, be greater than the maximum potential physiological stretching.
Another important parameter is the obliquity with which the force acts.

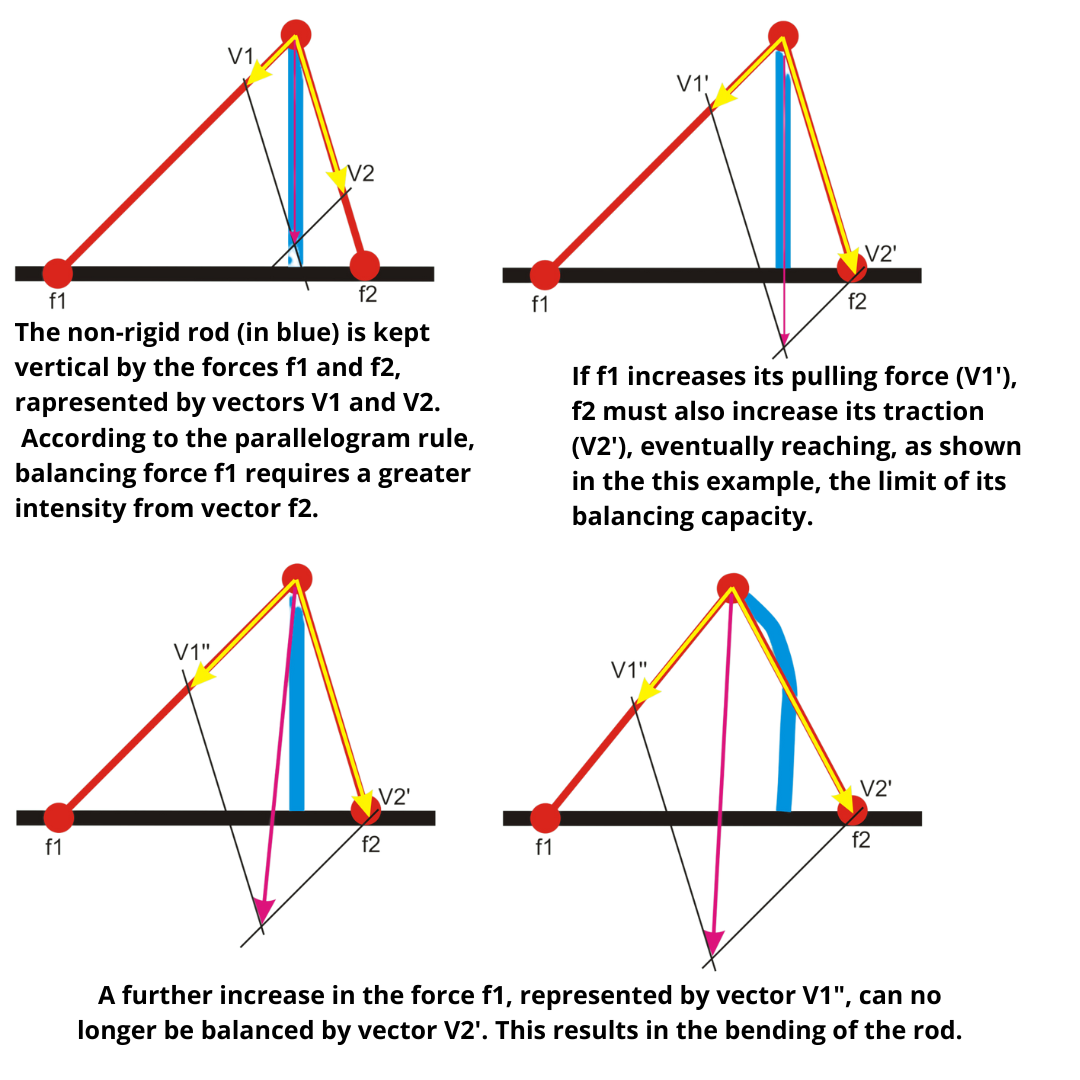
In the above figure, the verticality of the rod is ensured by the balance of two diagonal forces that, having different angular functions, use asymmetric intensities. The rod bends towards the force that is more oblique, when the vectorial balancing capacity of the diagonal force with the smaller angular function is exceeded.
If, on the rod, a diagonal force and a longitudinal force parallel to the rod act, the latter cannot balance the oblique force without stiffening the rod itself.

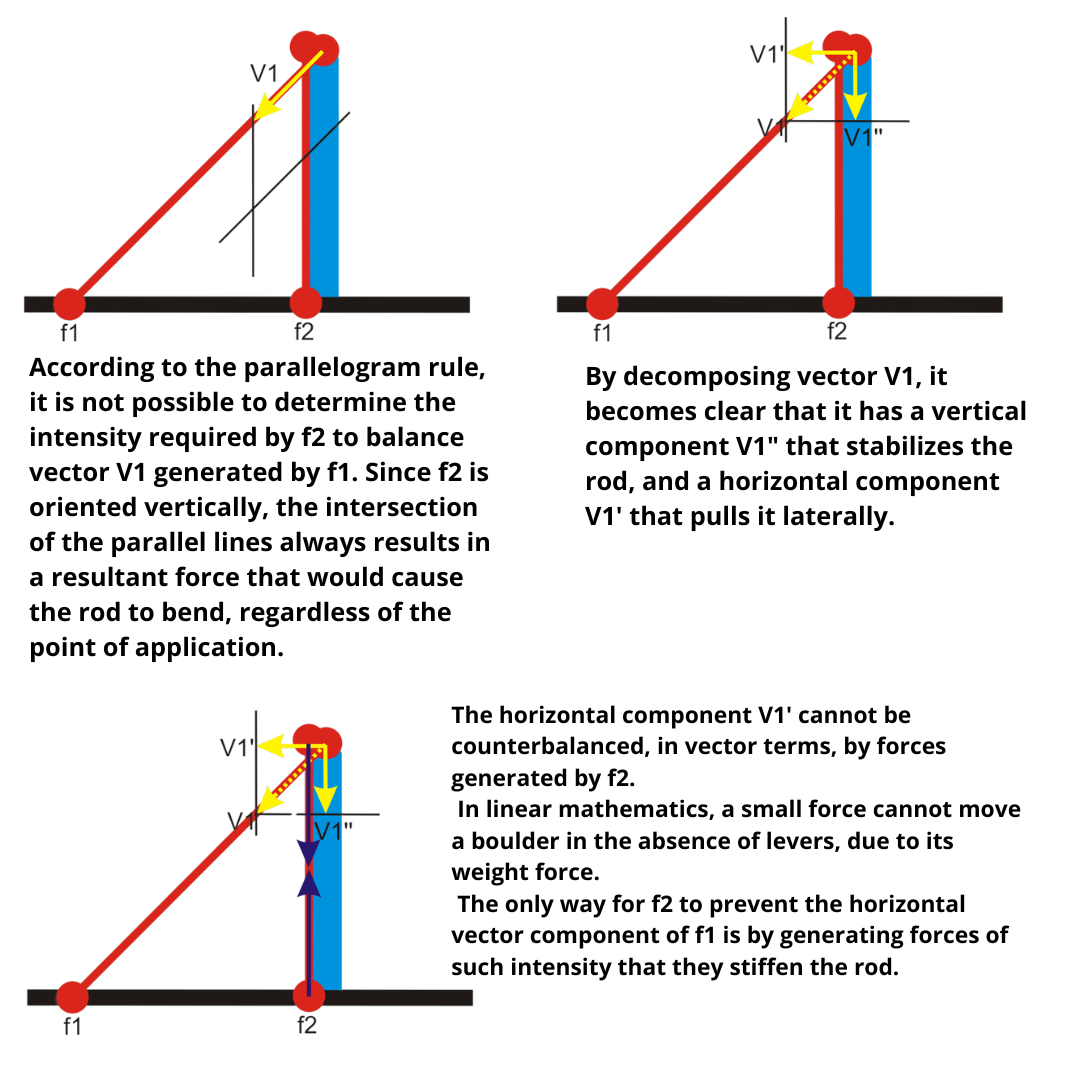
Compared to any dysmorphism, vector analysis tries to identify which force (muscle or muscle group) is favored in creating the observed pattern.

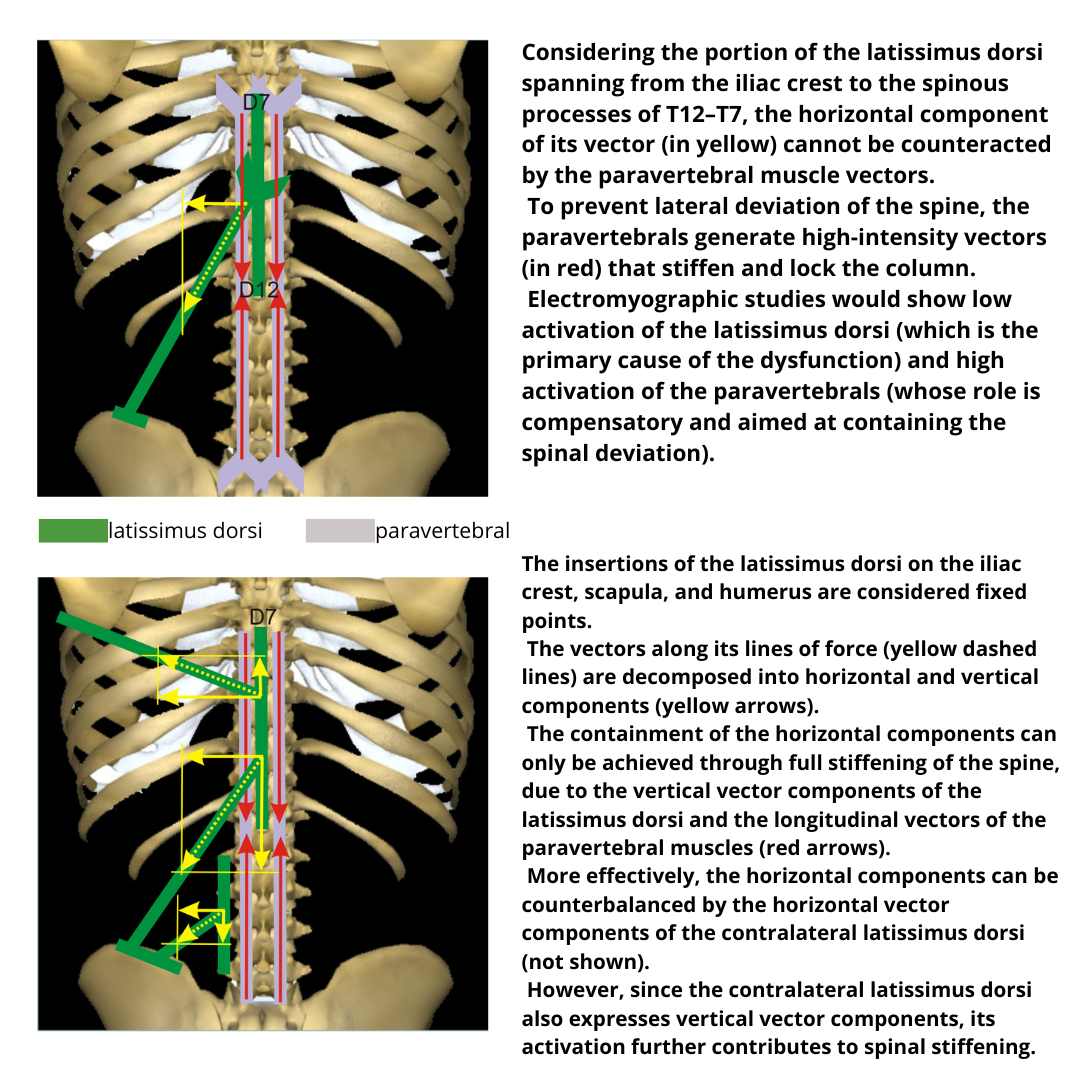
The drawings highlight how the increase in the vector intensity of an oblique force is potentially able to create greater skeletal displacement compared to a force having a longitudinal or oblique vector but with a smaller angular function. Moreover, the increase in tension of an oblique vector forces the longitudinal vectors to adapt by increasing the tensile force, in an attempt to balance the effect on the skeleton, blocking it.
We will see that, in almost all joints, muscle forces are vectorially asymmetric, meaning dominant and subdominant actions with respect to skeletal resultant forces.
For example, in the scapulohumeral relationship, the adduction of the humerus is dominant compared to abduction, as adductors are more numerous and have longer and more oblique vectors than abductors. The resultant vector of the adductors, if expressed at high intensity, cannot be balanced by the resultant vector of the abductors.
In vector logic and in the absence of peripheral neurological pathologies or other pathologies interfering with muscle contraction, subdominant actions will not be prevented or limited by the "weakness" of the agonist muscles, but by the excess tension of the antagonists. Referring to the previous example, it will not be the abductors of the humerus in hypo-contractile capacity (agonists of the action), but the adductors in excess tension that prevent the action (antagonists).
The following analytical treatment is not intended to be exhaustive but to provide interpretative tools adaptable to each individual case.
Moreover, not all potentially involved muscles will be examined, but only those vectorially most significant. In individual situations it may happen that the most probable vectors turn out negative: in such case a similar study procedure will be applied to minor vectors. In this case, the rules of linear mathematics (proportionality between stimulus and effect) will no longer apply, but those of nonlinear mathematics by which even small signals are able to produce significant changes.